Arreglos y matrices (2)

El concepto de herencias se puede entender con los arreglos.

A continuación, solo importando numpy, podemos hacer varias cosas con los arreglos, desde hacer auto llenados con ceros, unos, o valores random; diagonales, definir tamaño del arreglo, entre muchas otras más.

FORMA 1

#importando numpy para llenar matrices y mas
import numpy as np

#para solamente tener la librerias de np que son de arreglo
a=np.append([1,2,3],[[4,5,6],[7,8,9]])
print("primero",a)

#cuando se especifica el eje, valores
b=np.append([[1,2,3],[4,5,6]],[[7,8,9]],axis=0)
print(b)

#matrices
print(b.ndim)
#forma
print(b.shape)

#auto llenado
print()
a=np.arange(10) #0 ... n-1
print("primer autollenado",a)

b=np.arange(1,9,2) #inicio, final (excluido), paso
print("Llenado por eleccion",b)

c=np.linspace(0,1,6) #inicio, final, numero de puntos
print("Llenado de puntos",c)

d=np.linspace(0,1,5, endpoint=False) #no incluye el final
print("aun no se",d)
print()

#opciones
#llena de unos
a=np.ones((3,3))
print(a)
print()

b=np.zeros((2,2))
print(b)
print()

#llena diagonal principal con 1 y la forma es de 3
c=np.eye(3)
print(c)

#llena la diagonal principal con los valores dados
d=np.diag(np.array([1,2,3,4]))
print(d)
a=np.random.rand(4)
print(a)
#arreglo con dimension de 4
b=np.random.randn(4)
print(b)

d=np.array([1+2j, 3+4j, 5+6*1j])
print(d.dtype)

e=np.array([True, False, False, True])
print(e.dtype)

f=np.array(['Bonjour','hello','hallo'])
print(f.dtype) #unicode, version 7

a=np.diag(np.arange(3))
print(a)

a[1,2]=10 #tercera fila, segunda columna
print(a)
a=np.arange(10)
print(a)

a=np.arange(12).reshape(3,4)
print(a)

i=np.array([[0,1],[1,2]])
a[i,2] #lo mismo es a[i,2*np.ones((2,2),dtype=int)]
print(i)
#array([[2,6],
#  [6,10]])

• Ejecución:

FORMA 2

#usando matrix para realizar operaciones con matrices, como suma, resta, division

import numpy as np

from numpy import matrix

b=np.array([[0,1,2],[3,4,5]])

print(b)

print(b.ndim) #numero de corchetes al principio indica la dim

print(b.shape)

print(len(b))

print()

c=np.array([[1,2,3],[4,5,6],[7,8,9]])

print(c)

print(c.ndim)

print(c.shape)

print(len(c))  #la longitud da el numero de renglones

print()

d=np.array([[[1], [2]], [[3],[4]]])

print(d)

print(d.ndim)

print(d.shape)

print(len(d))

print()

print('sumas',' ','multiplicacion')

a=np.array([1,2,3,4])

print(a)

a=a+1

print(a)

a=a*3

print(a)

x1=np.array([[[1,2,3],[3,4,5]],[6,7,8]])

y1=np.array((1,2,3))

print('de x',x1.ndim)

print('de y',y1.ndim)

print('operadores')

a= np.array([1,1,0,0], dtype=bool)

b= np.array([1,0,1,0], dtype=bool)

print(a|b)

print(a&b)

print(a^b)

x=np.array([1,2,3,4])

print(x.sum())

print('suma renglon y columna')

x=np.array([[1,1],[2,2]])

print(x)

#por columna

print(x.sum(axis=0)) #se suman los ejes verticales (columnas)

#por renglon

print(x.sum(axis=1)) #se suman los ejes horizontales (renglones)

print('multiplicacion')

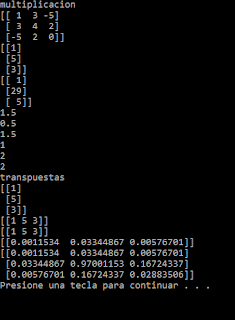
a=matrix([[1,3,-5],[3,4,2],[-5,2,0]])  #con matrix hace la multiplicacion directo

print(a)

b=matrix([[1],[5],[3]])

print(b)

a=a*b

print(a)

#estadistico

#desviacion media

print(x.mean())

#desviacion estandar

print(x.std())

print(np.median(x))

print(x.min())

print(x.max())

#indice del maximo

print(np.argmax(x))

#algebra lineal basica

print('transpuestas')

b=matrix([[1],[5],[3]]) #como esta con items individuales se hace una columna

print(b)

print(b.T) #imprime transpuesta

print(b.H) #Se calcula la hermitica (transpuesta conjugada)

c=a.I #Se calcula la inversa

print(c)

print(a*c) #se multiplica las matrices a y c

• Ejecución: