Operaciones algebraicas (6)

Con sympy se puede realizar cálculos con números complejos, y además puede simplificar operaciones trigonométricas.

Además, si queremos saber el valor real de una operación se utiliza .evalf().

Para saber el valor absoluto de una operación se pone abs(variable), el conjugate no resuelve la operación, solo la simplifica. Y si utilizamos arg(variable) nos dice el argumento del cálculo.

Cuando importamos Symbol, y ponemos x=Symbol('x', real =True) quiere decir que la variable simbólica sera la x.

Tambien con sympy se pueden encontrar raíces complejas de polinomios con la función solve(),

Con expand permite agregar cálculos (a una operación ya dada) con números complejos, trigonométricos, potencias, etc.

El numero e (Euler) se da con la letra E, y su parte real es re.

FORMA 1
#uso de abs, conjugate y evalf
from sympy import arg , conjugate ,sqrt ,I
#from math import *
#no resuleve  la operación la deja solo simplificada 
#sin comentario de math entonces da un resultado #numérico
a= sqrt (3)+I
print(conjugate (a))

print(abs(a))
print(arg(a))

#el valor real de alguna de las operaciones efectuadas
c=arg(a). evalf ()

print(c)

• Ejecución:

FORMA 2
#uso de Symbol, E, I, re, expand
from sympy import Symbol ,E,I,re

x= Symbol ('x', real = True )
a=E **(I*x)
b=a. expand ( complex = True )
print(b)
c=a **3
d=c. expand ( complex = True ). expand ( trig = True )
print(d)

print(re(d))
f=c. expand ( complex = True )
print(re(f))
res=(re(f)-re(d)). expand ( trig = True )

print(res)

• Ejecución:

FORMA 3
#algebra 4
from sympy import Symbol , solve
x= Symbol ('x ')
print(solve (x**4 -1 ,x))

• Ejecución:

FORMA 4

#Si el resultado esperado es amplio podemos guardarlo en una lista.

from sympy import Symbol , solve,I

x= Symbol ('x ')

print(solve (x**4 -1 ,x))

#es diferente

a= solve (x**4 -I,x)

print(a)

• Ejecución:

FORMA 5

#bucle para obtener los valores numericos de cada una de las soluciones
from sympy import Symbol , solve,I

x= Symbol ('x ')

print(solve (x**4 -1 ,x))

#es diferente

a= solve (x**4 -I,x)

#print(a)

for b in a:
print(b.evalf())

• Ejecución:

FORMA 6

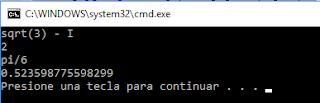
#uso de symplify para numeros complejos
#importar sympy
from sympy import I, simplify

print(simplify(((1+I) / (1+2 * I))))

• Ejecución: